dart 实现卡尔曼滤波

Kalman Filter

Kalman滤波被称为线性二次型估计。其也可以认为是一个最优化自回归数据处理算法（optimal recursive data processing algorithm）。前提是这个数据变化是线性变化的。

对于其原理我们可以参考Kalman Filter。文章写的很专业，我就不废话。

应用场景

当我们要观察一个仪器测量值，比如力度、重量等测量，在采集过程中，我们会不断拿到新数据，这些数据是采集器从目标中收集出来，是属于线性变化的。但采集器的精准度和目标物体的都含有不确定行。我们需要对这些数据进行过滤，生成平滑的数据。目标如下图：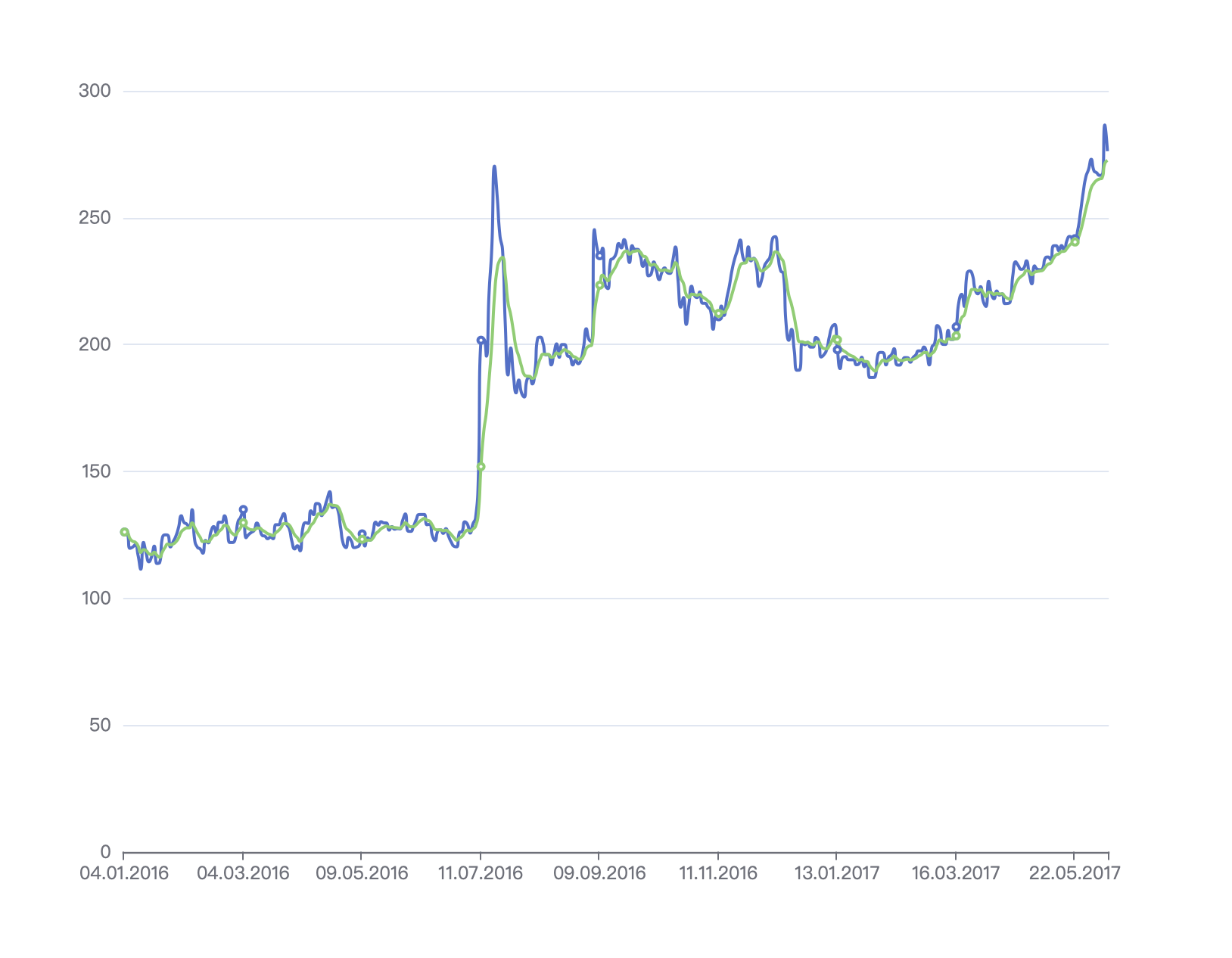

蓝线是原始数值，绿线是我们想要的结果。

Kalman Filter dart(Flutter)代码

class KalmanFilter {
  final double q; // 过程噪声协方差
  final double r; // 测量噪声协方差
  double x; // 当前状态
  double p; // 当前状态的协方差
  late double k; // 卡尔曼增益

  KalmanFilter({this.q = 0.1, this.r = 0.1, this.x = 0, this.p = 1});

  double update(double measurement) {
    // 预测步骤
    final x_pred = x;
    final p_pred = p + q;

    // 更新步骤
    k = p_pred / (p_pred + r);
    x = x_pred + k * (measurement - x_pred);
    p = (1 - k) * p_pred;

    return x; // 返回滤波后的值
  }
}

过程噪声协方差

它用来描述状态量在一个时刻到下一个时刻之间的变化幅度。一般来说，过程噪声方差是由系统的动态特性和采样间隔决定的。

如果系统的动态特性比较快，即状态量在一个时刻到下一个时刻之间的变化幅度比较大，那么过程噪声方差就应该设置得比较大，以便更好地反映状态量的变化。反之，如果系统的动态特性比较慢，即状态量在一个时刻到下一个时刻之间的变化幅度比较小，那么过程噪声方差就应该设置得比较小，以便更好地适应状态量的变化。

另外，采样间隔也会影响过程噪声方差的定义。如果采样间隔比较大，即状态量的变化相对较慢，那么过程噪声方差应该设置得比较小，以充分利用状态量的变化信息。反之，如果采样间隔比较小，即状态量的变化相对较快，那么过程噪声方差应该设置得比较大，以避免过度拟合状态量的变化。

因此，过程噪声方差的定义需要考虑系统的动态特性和采样间隔，需要进行实验和分析来确定最佳值。一般来说，过程噪声方差可以通过试验和经验得到，也可以使用自适应卡尔曼滤波器来自动调整。

观测噪声协方差

观测噪声协方差用来描述测量噪声对状态估计的影响。通常情况下，观测噪声协方差是由测量设备的精度和信噪比等因素决定的。

如果测量设备的精度越高，即测量误差越小，那么观测噪声协方差就应该设置得比较小，以更准确地反映状态量的真实值。反之，如果测量设备的精度较低，即测量误差较大，那么观测噪声协方差就应该设置得比较大，以充分考虑测量误差的影响。

另外，信噪比也会影响观测噪声协方差的定义。如果信噪比越高，即信号强度比噪声强度高，那么观测噪声协方差就应该设置得比较小，以更好地反映状态量的真实值。反之，如果信噪比较低，即信号强度比噪声强度低，那么观测噪声协方差就应该设置得比较大，以充分考虑噪声的影响。

因此，观测噪声协方差的定义需要考虑测量设备的精度和信噪比等因素，并且需要根据具体的应用场景进行实验和分析来确定最佳值。一般来说，可以通过实际测量数据的分析和处理来估计观测噪声协方差的值。

基础使用

// 初始化
 final kalmanFilter =
      KalmanFilter(q: 0.01, r: 0.1, x: originDatas.first.toDouble(), p: 1);
// 接收过滤结果
  List<double> fitterRes = []; 
  for (final measurement in originDatas) {
    final filteredMeasurement = kalmanFilter.update(measurement.toDouble());
    fitterRes.add(filteredMeasurement);
  }

上面这个代码片段只是简单过滤一组数据。在真实使用中当前状态协方差p和卡尔曼增益k会在每次检测流程中根据历史调整，而不是每次update的时候新建。所以是最好是通过一个单例的管理类去管理每次检测流程。